The basis function models (BMs) is a computational framework for modeling expressive music performance. This framework uses numerical encodings of musical scores (which we call basis functions) to learn from human music performances how music is performed in an expressive manner.
The Basis Mixer is an implementation of the BM framework. After it has been trained, it can be used to synthesize expressive performances of musical scores.

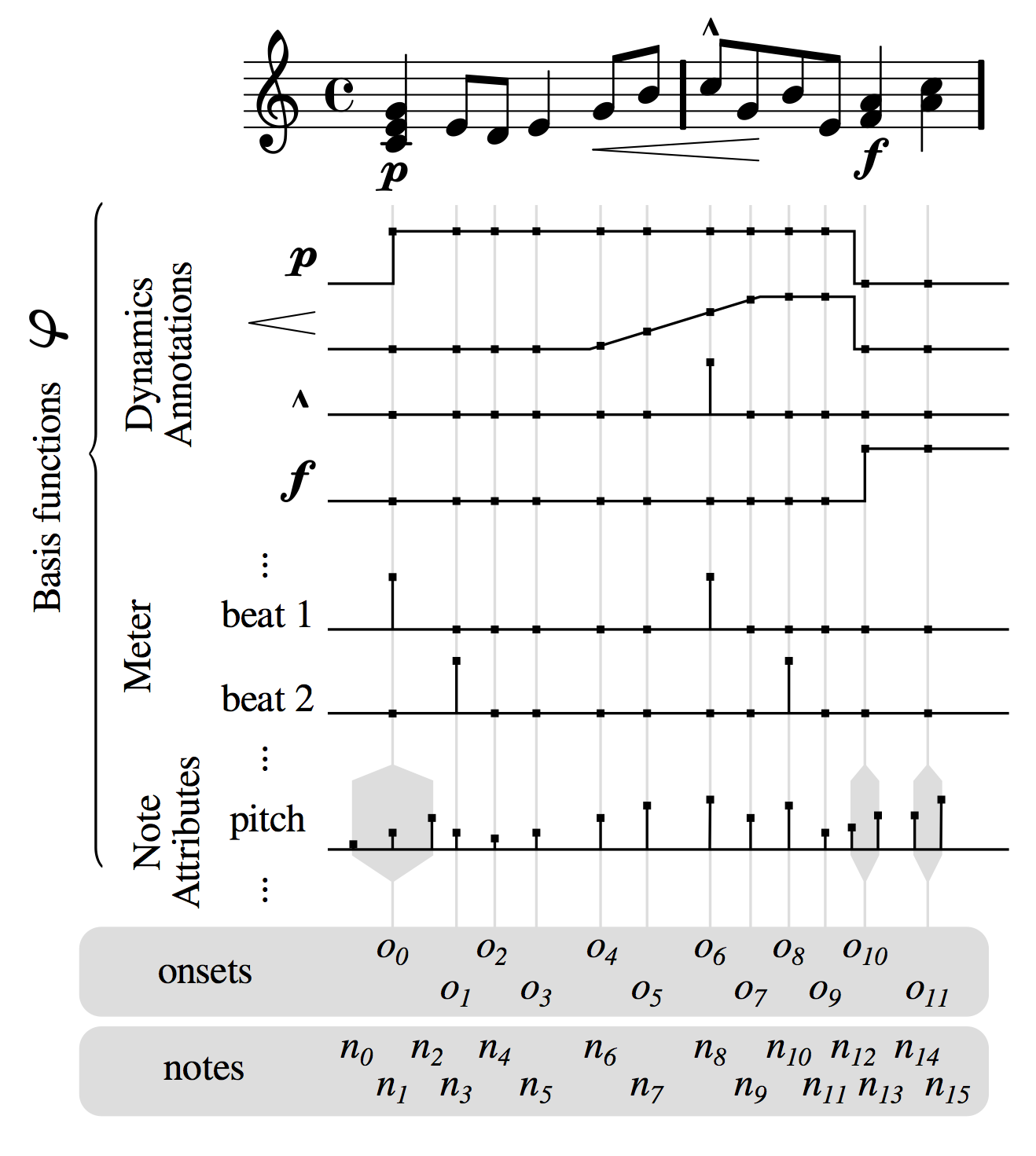
The BM framework models numerical descriptors that encode an expressive performance, referred to as expressive targets \(\boldsymbol{t}\), as a function of basis functions \(\boldsymbol\varphi\), i.e. numerical encodings of a variety of descriptors of the score. In its original formulation, the BM included mostly features accounting for performance directives explicitly written in the score like pitch, dynamics markings (such as \(\boldsymbol{\mathit{piano}}\) or \(\boldsymbol{\mathit{forte}}\)) and articulation markings (legato slurs, etc.) Recent work includes raw information form the piano roll, as well as musicologically informed features such as harmonic tension features, and features representing segmentation structure within the piece, based on a self similarit matrix of the piano roll. To the best of our knowledge, this diversity of score information is unprecedented in existing modeling approaches to musical expression.
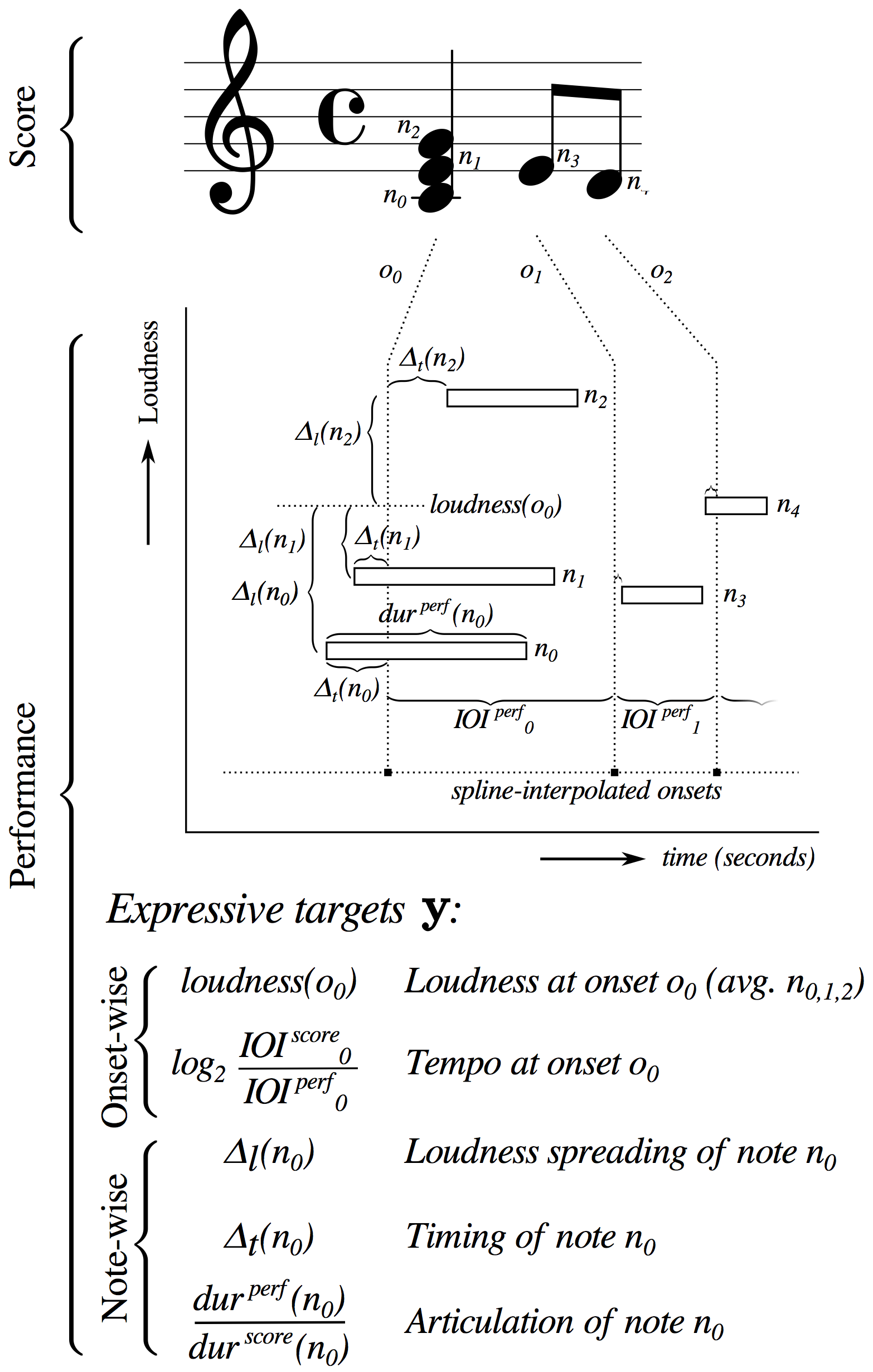
Loudness: Dynamics refers to the loudness of the performance. For simplicity we treat the MIDI velocity of the performed notes as proxy for dynamics. This parameter is then computed as the average MIDI velocity for all notes performed with the same onset
Tempo: Musical tempo is defined as the rate at which musical beats occur. Rather than the beat rate, we take the logarithm of its reciprocal, the beat period, as a representation of the local tempo. We compute the beat periods using a spline smoothing of the interonset intervals (IOIs).
Loudness spreading: Deviation of the MIDI velocity from the above temporal aggregate for each note in the time-step.
Timing: Onset deviations of the individual notes from the spline interpolation.
Articulation. Logarithm of the ratio between the actual duration of a performed note to its reference (notated) duration according to the local tempo.
This representation allows for a lossless reconstruction of a MIDI performance up to the average beat period. This is a desirable property for systems of expressive performance, since it means that a model with zero perdiction error (as measured by the mean squared error), will generate exactly the same performance it is trying to predict.
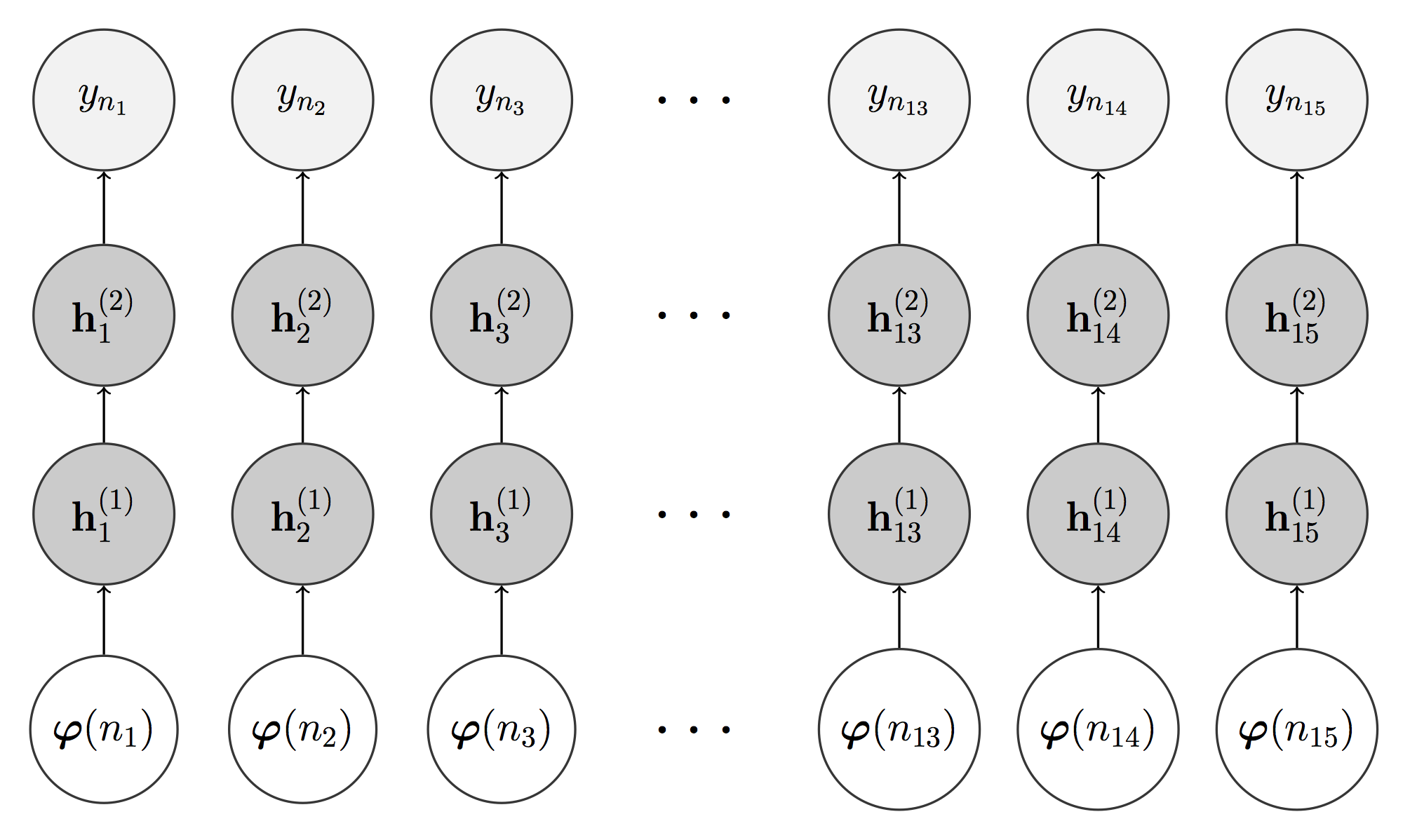
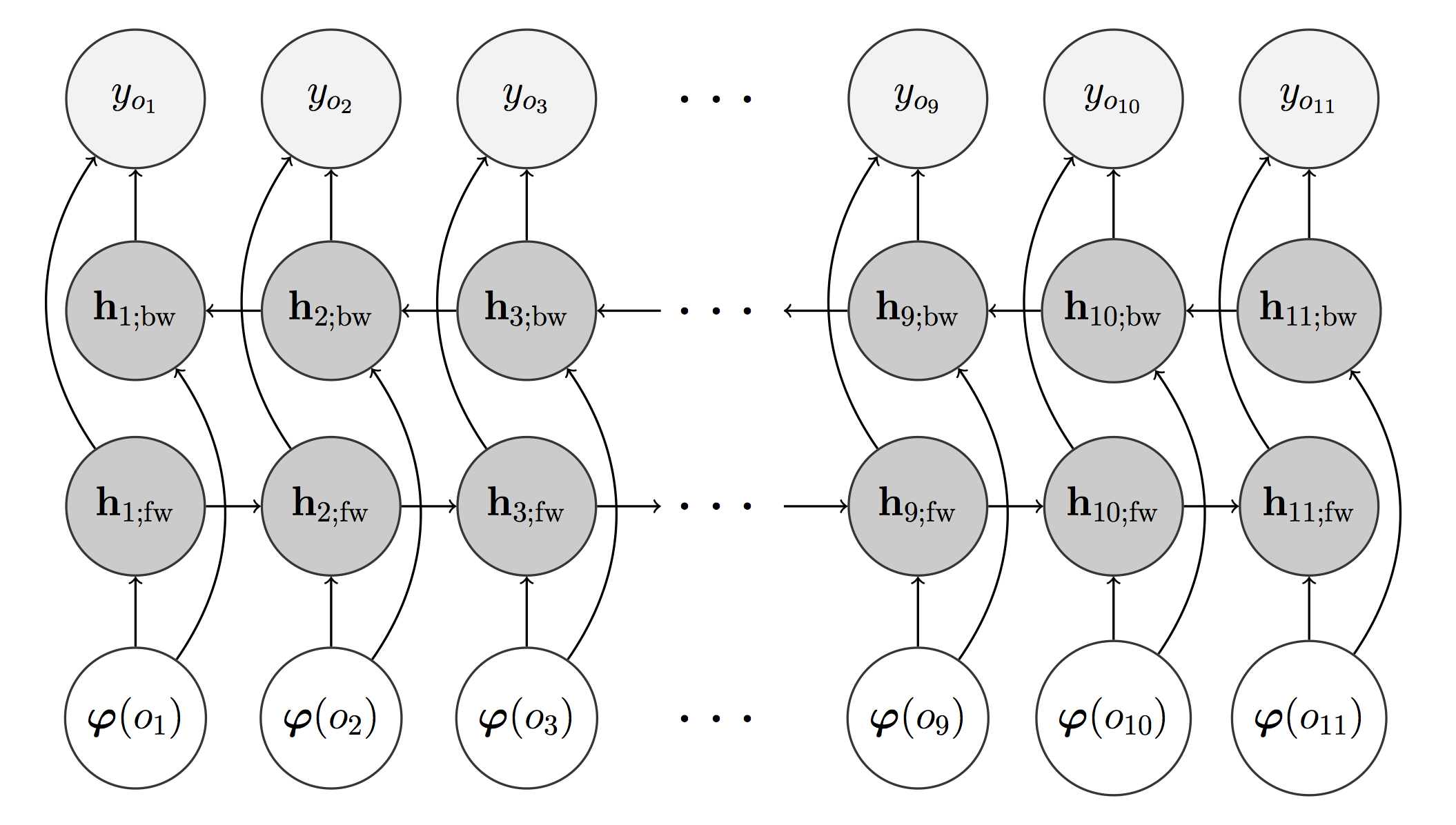
For rendering an expressive performance, we standardize the predictions of the parameters (i.e. we make them zero mean, unit variance). The user can then specify the mean value and standard deviation of each parameter.
expressive version
deadpan version
expressive version
deadpan version